311 Irani Oxi Engineering Complex
Department of Mechanical Engineering, Faculty of Engineering and Architecture, American University of Beirut
Gas-Structure Interaction in Microdevices: Simulation 3D DSMC Simulation of Gas Flows in Complex Domains
Investigators
issam lakkis, principal investigator
Mirvat Shamseddine, Ph.D. Candidate
An efficient Direct Simulation Monte Carlo (DSMC) FORTRAN code for performing three-dimensional simulations of low-density fluid flows over complex geometries is developed. The basic idea of DSMC is very simple. Millions of particles dynamically flow into the simulation domain, move independently to new positions where their movement includes treatment of boundary conditions. The computational domain itself is divided into grid cells that are utilized to select particles for collision on a probabilistic base and to sample various thermodynamic flow properties. However, these 3D simulations are relatively challenging and time-consuming and require a flexible data structures and an efficient particle-tracing scheme to reduce the amount of time required to achieve high performance solution for analyzing rarefied flows.
Hierarchical octree-based Cartesian grid is implemented where complex 3D physical objects with triangulated surfaces can be embedded in the grid. The derived data structure in Fortran 90 is adopted to efficiently store and manage the complete information related to the millions of particles, grid cells, and triangular surface elements during a DSMC simulation. This complex data structure is used to collect different elementary data structures such as variables, pointers, linked lists, and arrays together into one data structure. The hybrid mesh scheme accurately identifies body surfaces’ distribution within the three-dimensional grid cells, provides much flexibility in developing an efficient particle-tracing algorithm, accurately allows fluid-structure simulations, and dramatically reduces the amount of time required to obtain accurate results. The code is designed to be easy to modify or extend with new functionality.
Highlights:
-
3D DSMC for gas flows in the non-continuum regime
-
Complex Geometries
-
Ray Tracing
-
Fluid-Structure Interaction

Benchmark test cases indicate that the DSMC algorithm has satisfactory accuracy for complex rarefied gas flows.
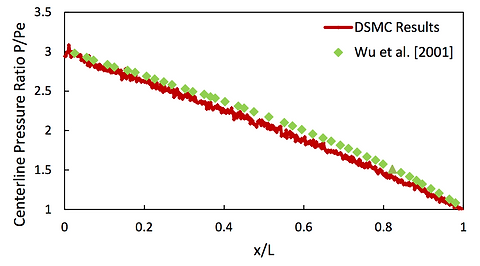
Centerline pressure profile for a Poiseuille flow
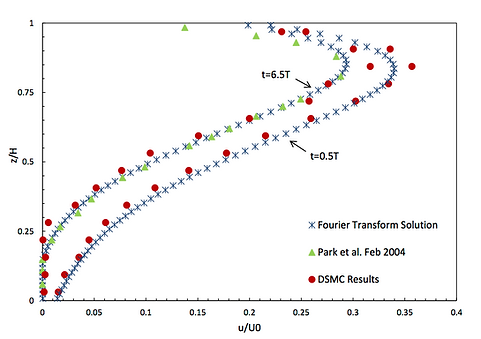
Normalized velocity for an oscillatory Couette flow
Investigation of the Dynamics of Gas-Structure Interaction in Microdevices using DSMC
Investigators
issam lakkis, principal investigator
Nadim Diab, Ph.D., 2012 (currently Chairman of the Mechanical Engineering Department at Harriri University)
-
Nadim A Diab and Issam A Lakkis. Investigation of the squeeze film dynamics underneath a microstructure with large oscillation amplitudes and inertia effects. Journal of Tribology, 138(3):031704, 2016.
Abstract
This paper presents direct simulation Monte Carlo (DSMC) numerical investigation of the dynamic behavior of a gas film in a microbeam. The microbeam undergoes large amplitude harmonic motion between its equilibrium position and the fixed substrate underneath. Unlike previous work in literature, the beam undergoes large displacements throughout the film gap thickness and the behavior of the gas film along with its impact on the moving microstructure (force exerted by gas on the beam’s front and back faces) is discussed. Since the gas film thickness is of the order of few microns (i.e., 0.01<Kn<1), the rarefied gas exists in the noncontinuum regime and, as such, the DSMC method is used to simulate the fluid behavior. The impact of the squeeze film on the beam is investigated over a range of frequencies and velocity amplitudes, correspond- ing to ranges of dimensionless flow parameters such as the Reynolds, Strouhal, and Mach numbers on the gas film behavior. Moreover, the behavior of compressibility pressure waves as a function of these dimensionless groups is discussed for different simulation case studies.
Conclusion
The dynamic force on a microbeam oscillating above a sub- strate imparted by a surrounding medium is investigated for a range of oscillating speed amplitudes and frequencies. The micro- flow behavior of the gas film between the beam and the substrate and its relation to the forces acting on the front and back sides of the beam are interpreted in terms of the relative contributions of diffusion and the unsteady and convective components of inertia, as quantified by the various dimensionless groups. It has been observed that for larger values of Reynolds number (i.e., inertia effects), the force on the side of the beam facing the substrate (front face) departs from the harmonic profile of the beam motion and the force amplitude on both beam faces during the first half period is larger than their counterparts during the second half period. For small Strouhal number, the phase difference between the beam and flow within the gap decreases. When Re and St are small, diffusion plays a dominant role over inertia, increasing the phase difference between the beam’s motion and front face force and decreasing the front face force amplitude. This corresponds to relatively low squeeze number where the gas has enough time to diffuse and escape from getting trapped between the oscillating beam and the fixed substrate. The compressible effects of the gas are shown to be dependent on the values of Ma2 and Ma2St2. It has been observed that when the beam oscillates at a low Ma, the pressure waves travel at a near sonic speed, while for high Ma the pressure wave speed approaches the speed of the beam itself. Finally, a 3D microbeam was simulated and the behavior of the pressure waves in its vicinity was compared to those of a 2D microbeam under the same conditions. The force distribution at the microbeam’s faces was plotted, and the effect of circulation around the beam’s tip was clearly indicated which plays a signifi- cant role in designing micro-RF switches especially at the point of contact (i.e., tip).
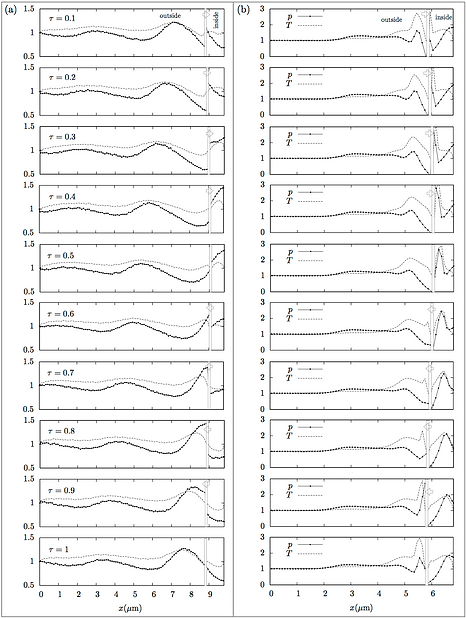
Normalized pressure and temperature distributions along plane of symmetry during a period of beam oscillation. Left: case (a) and right: case (b).

Evolution of normalized density distribution over a period of beam oscillation. Left: case (a), right: case (b).
Pressure profiles of the gauge pressure variation over one period in the vicinity of the microplate oscillating at 400 m/s and 1 GHz
-
Nadim A Diab and Issam Lakkis. Modeling squeeze films in the vicinity of high inertia oscillating microstructures. Journal of Tribology, 136(2):021705, 2014.
Abstract
This work investigates the effect of various assumptions proposed by the classical Reynolds lubrication equation. In particular, a microplate oscillating at high frequencies (beyond cutoff) and high velocities leading to appreciable displacement within the film gap is studied. An analytical model is derived with special emphasis on the fluid’s inertia effect on the fluid/solid interface. By implementing the direct simulation Monte Carlo (DSMC) method, a numerical method for modeling rarefied gas flow, the analytically based model is adjusted for the force exerted by the gas on the oscillating micro-structure to capture various significant effects related to the fluid’s inertia, compressibil-
ity, stiffness, and damping.
Conclusion
This work presents a combined analytical/numerical technique to develop a new force model for the squeezed film damping force in the vicinity of oscillating microstructures. For the analytical approach, an inviscid and incompressible problem is solved to stress the effect of the inertia on the fluid damping force and, therefore, new terms that reflect the contribution of inertia which are neglected in the classical Reynolds lubrication equation have been formulated. In addition, the DSMC method has been implemented to numerically correct for the proposed model (i.e., to include the viscous and compressibility effects) and, therefore, a more comprehensive damping force model was proposed. The coefficients of the proposed model were plotted to show their dependence on the set of the dimensionless groups governing the fluid behavior.

-
Nadim Diab and I. Lakkis. Dsmc simulations of squeeze film under a harmonically oscillating micro rf switch with large tip displacements. In Proceedings of ASME 2012 International Mechanical Engineering Congress and Exposition. ASME, 2012.
-
Nadim Diab and I. Lakkis. Dsmc simulations of squeeze film between a micro beam under- going large amplitude oscillations and a substrate. In ASME 10th International Conference on Nanochannels, Microchannels, and Minichannels. ASME, 2012.